3. Nullen und Einsen

3.1 Wir bauen einen einfachen Computer

Bleiben wir der Einfachheit halber bei einer Lampe, die wir mit einem Schalter ein- und ausschalten können. Fertig ist unser Computer!
"Wie bitte? Was soll daran ein Computer sein?" wirst du dich fragen.
Nun ja, er kann noch recht wenig, nämlich nur anzeigen, ob wir den Schalter betätigt haben oder nicht; genau genommen sagt er nur, ob wir den Schalter eine gerade oder ungerade Anzahl Male betätigt haben, bzw. ob Strom durch die Lampe fließt oder nicht. Aber immerhin: Wir können eine Zahl eingeben! Wenn wir den Schalter schließen geben wir eine Eins ein, wenn wir ihn nicht betätigen, geben wir eine Null ein; so legen wir das hier einfach mal fest. Und der Computer teilt uns eine Zahl mit (man sagt auch: Er gibt eine Zahl aus.): Wenn die Lampe brennt, gibt er eine Eins aus, wenn sie nicht leuchtet, gibt er eine Null aus - und wenn wir vergessen haben, den Strom anzuschließen, könnte das ausgegebene Ergebnis falsch sein!
Abbildung 1 und Abbildung 2 zeigen dir das ganze noch einmal als einfaches Bild.

Eine Lampe leuchtet immer dann, wenn der Strom durch ein Kabel bis zu ihr hin fließen kann. In Wirklichkeit muss er auch durch ein zweites Kabel wieder zurückfließen können, aber wir nehmen an, dass das immer der Fall ist und lassen dieses zweite Kabel in den Bildern einfach weg, damit es etwas übersichtlicher wird.

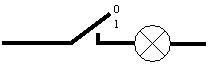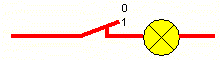
Abbildung 1: Schalter ein (er steht auf 1) die Lampe leuchtet	Abbildung 2: Schalter aus (er steht auf 0) die Lampe leuchtet nicht

Fällt dir auf, dass wir in diesem einfachen Computer sogar zwei verschiedene Möglichkeiten verwendet haben, die Zahlen Null und Eins darzustellen? Der Schalter kann offen oder geschlossen sein - er stellt die Zahl dar, die wir eingeben - und die Lampe kann leuchten oder nicht - sie stellt die Zahl dar, die der Computer uns ausgibt!

Nun wirst du bestimmt schon ungeduldig, denn unser Computer soll ja rechnen!
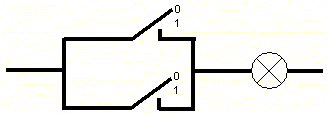
Auch dabei wollen wir wieder ganz einfach anfangen: Das einfachste Rechnen ist das Addieren (zusammenzählen, "plus" rechnen, "und" rechnen) von zwei Zahlen. Oh! Zwei Zahlen! Bisher können wir nur eine Zahl eingeben. Wir müssen unseren Computer also erweitern! Die zweite Zahl wollen wir genauso eingeben wie die erste, nämlich mit einem Schalter. Das Ergebnis der Rechnung lassen wir wieder mit der Glühlampe anzeigen. Abbildung 3 zeigt dir einen solchen Computer:

Abbildung 3: Computer, der zwei Zahlen addieren kann

So wie unser Rechner dort gezeichnet ist, haben wir ihm die Aufgabe gegeben, Null plus Null zu rechnen, denn der obere Schalter ist offen, die eine Zahl die wir eingeben ist also Null, und beim unteren Schalter ist es genauso. Und was hat unser Computer ausgerechnet? Es gibt kein durchgehendes Kabel vom linken Ende der Zeichnung bis zur Lampe, sie leuchtet also nicht. Also ist das ausgegebene Ergebnis Null! Das stimmt! Hurra!

Aber halt! Was ist, wenn wir eine andere Aufgabe rechnen, zum Beispiel 0 + 1 = ? Übersetzt in die Sprache unseres Computers bedeutet diese Aufgabe: Ein Schalter ist offen (Null) und einer ist geschlossen (Eins), wie es in Abbildung 4 gezeigt ist:

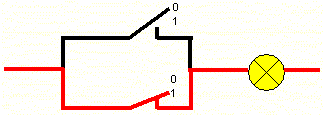Abbildung 4: Der Computer rechnet 0 + 1

Der Strom kann von links über den unteren Schalter bis zur Lampe fließen. Sie leuchtet! Der Computer sagt also "1"! Das Ergebnis ist wirklich Eins! Richtig!

Wie wäre es, wenn wir 1 + 0 rechnen wollten? Nun das kannst du dir leicht überlegen: Wir würden den oberen Schalter schließen und der untere bliebe offen; der Strom könnte dann über den oberen Schalter bis zur Lampe fließen und sie würde auch leuchten! Auch dann wäre das Ergebnis richtig!

Und was ist, wenn wir 1 + 1 rechnen wollen? Dann würden wir den oberen und den unteren Schalter schließen. Die Lampe würde leuchten, der Computer gibt also das Ergebnis "1" aus! 1 + 1 = 1, was ist denn das für ein Quatsch! Das richtige Ergebnis wäre doch Zwei!

Was ist denn jetzt falsch gelaufen? Warum gibt unser Computer nicht "2" aus? - Ganz einfach: Er kann es nicht! Er kann es nicht, weil sein Ausgabegerät, sein "Bildschirm", die Lampe, nur die Zahlen Null und Eins anzeigen kann, indem sie aus oder an ist. Die Zahl Zwei kennt unser Computer noch nicht!

Wie könnten wir ihm das beibringen? Das mit der Null und der Eins hat ja bisher ganz gut geklappt und es wäre doch schön, wenn unser Computer damit auskommen würde!?

Nun, wir Menschen benutzen zehn Ziffern: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Wir können aber doch trotzdem größere Zahlen darstellen als Neun. Also muss es doch auch möglich sein, mit zwei Ziffern größere Zahlen als Eins darzustellen! Wenn wir größere Zahlen als Neun darstellen wollen, also zum Beispiel "Zwölf", dann helfen wir uns, indem wir eine weitere Ziffer an einer zweiten Stelle dazuschreiben: 12!

Jedes Mal wenn wir bei der ersten Stelle (der rechten) keine Ziffern mehr haben, um weiter zu zählen, dann erhöhen wir die zweite Stelle (die linke) um Eins. Also: Bis Neun haben wir genügend Ziffern, um mit einer Stelle auszukommen; wenn wir dann weiter zählen wollen, schreiben wir "10". Wir erhöhen also die zweite Stelle um eins - und fangen bei der ersten Stelle wieder mit Null an!

Die Stellen einer Zahl werden in diesem Buch von rechts nach links gezählt, weil man die rechte Stelle beim Zählen als erstes braucht, und die anderen erst danach hinzukommen.

Man kann das sehr schön am Kilometerzähler eines Autos sehen: Wenn das Auto fährt, verändert sich nur die rechte Stelle und zählt die Kilometer (bei manchen Autos werden ganz rechts die Hektometer (=100m) gezählt). Sobald an der rechten Stelle die 9 erscheint, wird beim nächsten Weiterzählen die zweite Stelle eins weiter gezählt und an der ersten Stelle erscheint wieder die Null.

Genauso könnte das doch auch unser Computer machen: Nehmen wir an, er würde zählen. Null bedeutet, die erste Lampe ist aus; Eins bedeutet, die erste Lampe ist an; jetzt kann er nicht mehr weiter und braucht eine zweite Stelle, also eine zweite Lampe. Zwei bedeutet also, die neue linke Lampe ist an - und die erste Lampe muss wieder bei Null anfangen, genau wie der Kilometerzähler; die erste Lampe muss also wieder ausgehen, wenn die zweite angeht.

Die folgende kleine Tabelle zeigt dir, wie unser Additionscomputer die Ergebnisse von 0 bis 2 mit zwei Lampen darstellen soll:

Schalter 1	Schalter 2	Additions- ergebnis	Zweite Lampe	Erste Lampe
Null	Null	0
Null	Eins	1
Eins	Null	1
Eins	Eins	2

Tabelle 1: Mit zwei Lampen Ergebnisse von 0 bis 2 ausgeben

Wenn die Schalter so stehen wie in den ersten beiden Spalten gesagt, dann soll das Ergebnis der Addition (mittlere Spalte) mit den zwei Lampen so dargestellt werden, wie in den rechten beiden Spalten gezeigt.

Fangen wir mit der ersten Lampe an. Die Verschaltung dafür haben wir zwar schon in Abbildung 3 und Abbildung 4 fertig gehabt, aber wegen des falschen Ergebnisses bei unserer 1 + 1 Aufgabe müssen wir daran wohl etwas ändern:
Die Lampe soll aus bleiben, wenn beide Schalter gleich stehen (00 oder 11), und sie soll leuchten, wenn sie unterschiedlich stehen (01 oder 10).
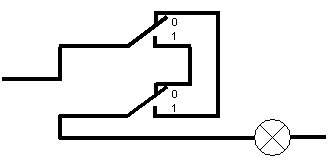
Das geht mit der Schaltung wie sie in Abbildung 5 gezeigt wird. Dabei bauen wir die Schalter etwas um: Sie schalten den Strom jetzt nicht ein oder aus, sondern sie schalten ihn von einem Kabel auf ein anderes um. Trotzdem haben sie nur zwei Schalterstellungen entsprechend Null und Eins: Hebel oben entspricht Null, Hebel unten entspricht Eins.

Abbildung 5: Kein Kabelweg geht bis zur Lampe durch. Sie leuchtet deshalb nicht.

Abbildung 5 zeigt den Zustand, dass beide Schalter auf Null stehen. Du wirst kein Kabel finden, das bis zur Lampe durchgeht. Sie leuchtet also nicht und bedeutet damit "Null". Vergewissern wir uns mit Tabelle  1: Wenn beide Schalter auf Null stehen, soll die rechte Lampe nicht leuchten, für diesen Fall ist unsere Schaltung also richtig!

Was ist nun, wenn ein Schalter auf Eins steht?
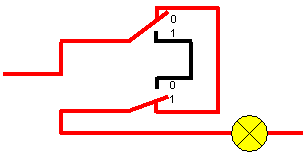
Dieser Zustand wird in Abbildung 6 gezeigt:

Abbildung 6: Die Lampe leuchtet, weil es einen durchgehenden Kabelweg gibt.

Der untere Schalter steht auf "Eins" und dadurch gibt es einen durchgehenden Kabelweg zur Lampe und sie leuchtet. Du kannst dir an Hand des Bildes schnell überlegen, dass die Lampe auch dann leuchtet, wenn der obere Schalter auf "Eins" und der untere auf "Null" steht. (Falls du Schwierigkeiten hast, male dir die Schaltung selbst noch einmal auf!)

Wenn beide Schalter auf "Eins" stehen, gibt es wieder keinen durchgehenden Kabelweg, so dass die Lampe dann nicht leuchtet. Wenn wir noch mal in Tabelle 1 schauen und kontrollieren, stellen wir fest, dass unsere Lampe Nummer eins nun genau das tut, was sie soll: Sie leuchtet immer dann, wenn entweder der eine oder der andere Schalter auf "Eins" steht und Sie leuchtet nicht, wenn beide Schalter gleich stehen, also beide auf "Null" oder beide auf "Eins".

Eine solche Schaltung findest du bestimmt auch in eurer Wohnung! Meistens gibt es sie an Treppen oder in Räumen mit mehr als einer Tür (meist ein Flur). Man nennt sie auch "Wechselschaltung".

Nun sind wir ein wenig vom Thema abgeschweift! Wir wollten ja einen Computer mit einer zweistelligen Anzeige bauen! Dafür fehlt uns noch die Schaltung der zweiten Lampe! Sehen wir mal in Tabelle 1 nach: Diese Lampe soll nur leuchten, wenn beide Schalter auf "Eins" stehen. Das ist einfach:

Abbildung 7: Die Lampe leuchtet nur dann, wenn beide Schalter auf "Eins" stehen.

Du kannst dir an Hand von Abbildung 7 leicht überlegen, dass es einen durchgehenden Kabelweg erst dann gibt, wenn beide Schalter geschlossen sind.

Die beiden Schalter in Abbildung 5 und 6 sind natürlich die selben wie in Abbildung 7, denn wir geben ja nur zwei Zahlen ein! Das bedeutet, dass die dargestellten Kabelwege gleichzeitig geschaltet werden. Solche Schalter gibt es auch und in Abbildung 8 ist unser Computer noch einmal als Ganzes gezeichnet.

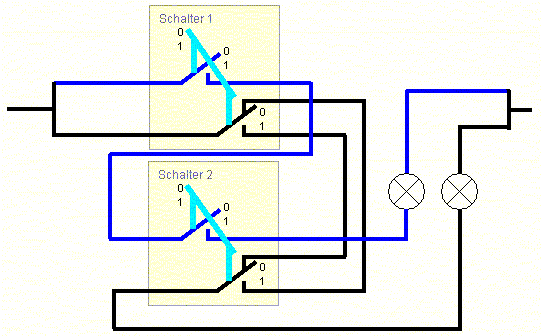
Abbildung  8: Wie die zwei Lampen mit den zwei Schaltern verbunden werden müssen, damit unser Computer richtig addiert

Die Schalter sind zur besseren Übersicht, was alles zu einem Schalter gehört, in dünnen Kästchen eingerahmt. In jedem Kästchen befinden sich zwei elektrische Schalter, die allerdings nur gleichzeitig betätigt werden können. Die hellblauen Bügel sollen das andeuten. Die Wechselschaltung für die erste Lampe (rechts) ist schwarz, die Verkabelung für die zweite Lampe (links) ist blau gezeichnet. In der abgebildeten Schalterstellung rechnet der Computer 0 + 0 und das Ergebnis ist Null, also richtig.

Dieser Computer kann nun wirklich die beiden Zahlen, die wir mit Hilfe der beiden Schalter darstellen, zusammenzählen! Je nachdem welche Zahlen wir an den beiden Schaltern einstellen, wird immer das richtige Ergebnis berechnet, wie wir es uns in Tabelle 1 überlegt hatten! Versuche an Hand von Abbildung 8 das zu überprüfen!

Bestimmt hast du immer noch das Gefühl, dass das noch kein richtiger Computer ist! Ganz Unrecht hast du damit natürlich nicht, denn ein Computer kann ja erstens mit viel mehr und viel größeren Zahlen rechnen und zweitens hast du ja im Kapitel 2 aufgepasst und gelernt, dass man einen Computer programmieren kann. Unser Computer rechnet aber immer nur zwei Zahlen zusammen und wir können ihm nicht sagen, dass er etwas anderes tun soll.

Jetzt bringen wir erst mal die Geschichte mit den größeren Zahlen zu Ende und später bauen wir dann auch noch einen Computer, der verschiedene Dinge tun kann!