3. Nullen und Einsen

3.2 Größere Zahlen

Denke noch einmal daran zurück, was wir gemacht haben, als wir die Zahl 2 mit unserer einen Lampe nicht darstellen konnten: Wir haben eine zweite Stelle eingeführt, die durch eine zweite Lampe dargestellt wurde. Können wir damit nur bis zwei zählen?

Wenn wir mit "richtigen" Zahlen zählen, kommt nach der 9 die 10, das heißt die zweite Stelle wird eingeführt. Dann kommt die 11, dann die 12, 13, 14, 15, 16, 17, 18 und dann die 19. Wir erhöhen also wieder so lange unsere erste (rechte) Stelle, bis wir erneut keine Ziffern mehr haben, um weiter zu zählen. Was machen wir dann? Wir erhöhen unsere zweite Stelle und setzen die erste wieder auf Null und heraus kommt die 20.

Genau so können wir es mit unseren beiden Lampen auch machen! Wenn wir bis zwei gezählt haben, können wir immer noch die erste Lampe wieder einschalten, so dass dann beide brennen, und wir haben bis drei gezählt. Für unseren zuvor gebauten Computer brauchten wir das nur deshalb nicht, weil wir ihm keine Aufgabe mit dem Ergebnis "Drei" stellen konnten.

Tabelle 2 zeigt dir die zwei Lampen, wie sie bis 3 zählen. Die Spalte "Bedeutung" übersetzt dir die Spalte mit den Lampenbildern: Eine brennende Lampe bedeutet Eins, und eine Lampe, die nicht brennt, bedeutet Null.

Zahl	Zweite Lampe	Erste Lampe	Bedeutung
0			0	0
1			0	1
2			1	0
3			1	1

Tabelle 2: Zählen mit zwei Lampen

Können wir mit zwei Lampen noch weiter zählen? Nein! Es gibt keine An/Aus-Kombination mehr, die noch eine weitere Zahl darstellen könnte! Es gibt vier Kombinationen, weil wir zwei Lampen mit jeweils zwei Möglichkeiten haben. Jeder dieser vier Kombinationen haben wir eine Zahl zugeordnet, nämlich die vier Zahlen von 0 bis 3. (Computerleute beginnen immer bei Null zu zählen!)

Du wirst dir schon denken, wie wir weiterzählen können: Wir führen eine dritte Stelle, oder - bei unserem Computer - eine dritte Lampe ein. Diese hat wieder zwei Möglichkeiten: Sie ist an oder aus. Bei jeder dieser beiden Möglichkeiten können wir die übrigen beiden Lampen in den vier Kombinationen aus Tabelle 2 leuchten lassen, so dass wir zwei mal vier gleich acht verschiedene Zahlen darstellen können. Wir können also mit drei Lampen von 0 bis 7 zählen! In Tabelle 3 steht, wie ein Computer mit drei Lampen zählen würde:

Zahl	Lampe 3	Lampe 2	Lampe 1	Bedeutung
0				0	0	0
1				0	0	1
2				0	1	0
3				0	1	1
4				1	0	0
5				1	0	1
6				1	1	0
7				1	1	1

Tabelle 3: Mit drei Lampen bis Sieben zählen

Nun kannst du dir vorstellen, dass wir zu den drei Lampen vorne auch noch Schalter dazubauen, mit deren Hilfe wir auch größere Zahlen eingeben können. Damit wir nicht wieder eine solche Überraschung erleben wie bei der Rechenaufgabe 1 + 1, bei der das Ergebnis so groß war, dass unser Computer es nicht anzeigen konnte, könnten wir zwei Schalter für die erste einzugebende Zahl vorsehen und zwei Schalter für die zweite. Jedes Schalterpaar könnte dann Zahlen zwischen 0 und 3 darstellen (vgl. Tabelle 1), so dass das größtmögliche Ergebnis 6 wäre; das könnten wir mit unseren drei Lampen wie in Tabelle 3 gezeigt darstellen.

Wenn wir uns jetzt vorstellen, wie diese insgesamt vier Schalter und drei Lampen zu verschalten wären, sehen wir nur noch einen ziemlichen Kabelsalat! Schon die Schaltung für zwei Lampen und zwei Schalter aus Abbildung 5 und Abbildung 7 war ja ziemlich unübersichtlich! Nun man kann das Ganze etwas geschickter lösen als wir es getan haben, und außerdem viel, viel kleiner; aber darauf komme ich später noch einmal zurück.

Für jetzt ist erst einmal klar, wie wir mit größeren Zahlen als Drei rechnen können. Auch Sieben ist noch keine so riesengroße Zahl, dass wir von unserem Computer beeindruckt sein könnten, aber wir haben das Prinzip verstanden: Wenn wir größere Zahlen darstellen wollen, nehmen wir einfach mehr Stellen! Nichts anderes machen wir mit unseren normalen Zahlen schließlich auch!

Mit jeder Stelle, die wir hinzufügen, verdoppeln wir die Anzahl der Zahlen, die wir darstellen können. Falls dir nicht klar ist warum, schaue dir Tabelle 3 noch einmal an.

Wenn du alles verstanden hast, kannst du sicherlich auch die Frage beantworten, wie viele verschiedene Zahlen man mit einer Hand darstellen kann!?
Fünf (1 bis 5)? Nein! Mehr!
Sechs (0 bis 5)? Schon besser! Aber es sind noch mehr! (Obwohl die meisten Menschen ihre Finger nur so benutzen.)
Denke daran, dass jeder deiner fünf Finger entweder ausgestreckt oder eingeklappt sein kann!
Man kann mit fünf Fingern 32 Zahlen darstellen! (In Worten: Zweiunddreißig, nämlich die Zahlen 0 bis 31)!
Okay, zugegeben: Es bedarf etwas Übung jeden einzelnen Finger unabhängig von den anderen zu bewegen, aber es geht!
Tabelle 4 zeigt dir wie:

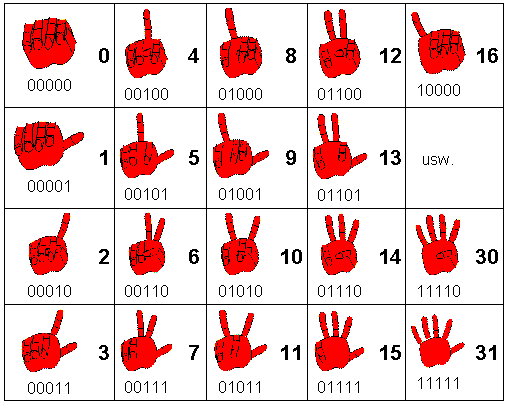
Tabelle 4: Mit den fünf Fingern einer Hand von 0 bis 31 zählen!

Die ersten Leute, die Computer gebaut haben, haben sich nicht mit drei Stellen ("Bits") zufrieden gegeben und auch noch nicht mit fünf. Sie haben immer acht Bits verwendet.
Damit kann man 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 2⁸ = 256 Zahlen darstellen. Das ist für heutige Verhältnisse auch noch nicht so furchtbar viel; heutige Rechner arbeiten mit 32 oder sogar 64 Bits gleichzeitig. Jedenfalls waren es zu Anfang acht Bits und deshalb hat man für solche Zahlen aus acht Bit ein eigenes Wort erfunden:

Acht Bit heißen ein Byte. Das spricht man beit aus.

Auch die frühen 8-Bit-Rechner konnten schon mit größeren Zahlen als 255 rechnen. Nur konnte eine solche Zahl dann eben nicht in einem Schritt verarbeitet werden, sondern sie musste in mehrere Teile zerlegt werden, mit denen nacheinander gerechnet wurde - wieder begegnet uns das Prinzip, schwierige Aufgaben in mehrere kleine zu zerlegen, um sie lösen zu können.