3. Nullen und Einsen

3.5 Bilder mit Nullen und Einsen

Jetzt können wir schon Zahlen und Texte mit Hilfe von Nullen und Einsen darstellen! Aber was machen wir mit Bildern? Du hast schon mal Bilder auf einem Computerbildschirm gesehen, also weißt du, dass es auch dafür eine Lösung gibt. Aber welche?

Können wir dem Computer wieder eine Zuordnung geben, also zum Beispiel "01101001" entspricht einem Baum auf unserem Bild? Wenn du Computer wärst, würdest du sofort fragen:

"Eine Tanne oder eine Eiche? Im Sommer oder im Winter? An welcher Stelle des Bildes?"

Du merkst, so klappt das noch nicht ganz! Aber die Idee, einem Byte wieder eine Bedeutung zuzuordnen, ist schon mal nicht schlecht, denn sie hat ja bereits zweimal funktioniert. Nur die Bedeutung "Baum" ist etwas ungeschickt gewählt! Wir müssen also wieder einfacher werden. Wir haben ja nur die 256 Möglichkeiten eines Bytes zur Verfügung, um unser Bild oder Teile davon zu beschreiben, und es gibt mit Sicherheit viel, viel mehr Möglichkeiten, einen Baum zu malen, ganz zu schweigen von Häusern, Autos, Menschen und Tieren. Der Teil des Bildes, den wir mit einem Byte beschreiben können, muss also viel kleiner sein als ein Baum. Und der Teil muss sich dazu eignen, aus mehreren davon sowohl einen Baum, als auch ein Auto, als auch alles mögliche andere zu malen.

Kennst du den Maler Vincent van Gogh? Abbildung 11 zeigt dir ein Bild von ihm, auf dem er sich selbst gemalt hat.

Abbildung 11: Selbstbildnis von Vincent van Gogh

Fällt dir daran etwas auf? Das Bild besteht aus ganz vielen kleinen Farbklecksen! Wenn du einen einzelnen Klecks davon siehst, kannst du nicht erkennen, ob er zu einem Baum, einem Menschen oder einem Auto gehört. Erst alle Kleckse zusammen ergeben das vollständige Bild. Das ist die Lösung unseres Problems! Der gute Vincent ist schon seit über hundert Jahren tot († 1890), und er hätte sich bestimmt nicht träumen lassen, dass es mal Maschinen geben würde, die Bilder nach dem selben Prinzip erzeugen wie er. In der Kunst nennt man diese Stilrichtung übrigens Impressionismus.

Da unser Computer kein Künstler, sondern - wie wir schon mehrfach gesehen haben - ziemlich dumm ist, müssen wir das Ganze noch ein wenig weiter vereinfachen, indem wir die Kleckse zur Darstellung eines Bildes erstens alle gleich groß machen und ihnen zweitens allen die gleiche Form geben. Was unterscheidet die Kleckse dann noch voneinander? Ach ja richtig: Die Farbe! Mit Hilfe unserer 256 Möglichkeiten die Bits eines Bytes zu schreiben, können wir nun die Farbe codieren.

Natürlich unterscheiden sich die Kleckse auch durch die Stelle, an der sie im Bild sitzen. Müssen wir die auch codieren?
Wir beschreiben ja auch nicht, wo das Byte 01000001 hingehört, das diesen Buchstaben A beschreibt. Das ergibt sich einfach aus der Reihenfolge der Bytes! Bei einem Bild ist es ganz genauso: Wir legen nur fest, wie viele Farbkleckse - vornehmer sagt man auch Bildpunkte oder Pixel - wir nebeneinander und wie viele untereinander brauchen, um ein Bild darzustellen, und wenn wir dann beispielsweise oben links in der Bildecke anfangen, und Zeile für Zeile jeden Farbklecks - pardon: Pixel - mit seiner Farbe beschreiben, haben wir unser Bild komplett mit Nullen und Einsen nachgebildet.

Das folgende ganz einfache Bild in Abbildung 12 soll dir das Prinzip verdeutlichen:

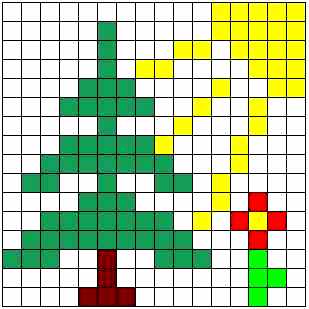Abbildung 12: Bild mit 256 Pixeln

Du erkennst einen Tannenbaum, eine Blume und die Sonne mit ein paar Sonnenstrahlen in diesem Bild. Es handelt sich um ein sehr grob gerastertes Bild: Es besteht nur aus 16 x 16 = 256 Bildpunkten, aber trotzdem kann man schon etwas erkennen!

Insgesamt habe ich fünf verschiedene Farben in dem Bild verwendet. Fünf? Nein sechs! Denn auch die Hintergrundfarbe weiß ist eine Farbe, die ich beschreiben muss! Ganz ähnlich wie wir in Tabelle 6 jedem Buchstaben eine Bitfolge zugeordnet haben, müssen wir es jetzt auch für die Farben tun! Tabelle 7 enthält eine willkürliche Zuordnung, die ich mir dafür überlegt habe.

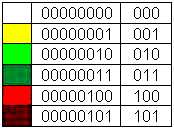
Tabelle 7: Farbcodierung

Eine solche Beschreibung aller verwendeten Farben nennt man auch eine Palette.

Da ich nur so wenig Farben verwendet habe, brauche ich nicht alle 8 Bit; die rechte Spalte zeigt daher nur die rechten drei Bits, auf die ich mich im Folgenden beschränken will, um mir Schreibarbeit zu sparen! Wenn wir jetzt das Bild mit Hilfe von Nullen und Einsen beschreiben wollen, tun wir das einfach, indem wir die Bitcodes für jede Farbe benutzen. Ich schreibe die Codes für jedes Pixel zeilenweise hin und beginne oben links. Kontrolliere es!

000 000 000 000 000 000 000 000 000 000 000 001 001 001 001 001
000 000 000 000 000 011 000 000 000 000 000 001 001 001 001 001
000 000 000 000 000 011 000 000 000 001 001 000 001 001 001 001
000 000 000 000 000 011 000 001 001 000 000 000 000 001 001 001
000 000 000 000 011 011 011 000 000 000 000 001 000 000 001 001
000 000 000 011 011 011 011 011 000 000 001 000 000 001 000 000
000 000 000 000 000 011 000 000 000 001 000 000 000 001 000 000
000 000 000 011 011 011 011 011 001 000 000 000 001 000 000 000
000 000 011 011 011 011 011 011 011 000 000 000 001 000 000 000
000 011 011 000 000 011 000 000 011 011 000 001 000 000 000 000
000 000 000 000 011 011 011 000 000 000 000 001 000 100 000 000
000 000 011 011 011 011 011 011 011 000 001 000 100 001 100 000
000 011 011 011 011 011 011 011 011 011 000 000 000 100 000 000
011 011 011 000 000 101 000 000 011 011 011 000 000 010 000 000
000 000 000 000 000 101 000 000 000 000 000 000 000 010 010 000
000 000 000 000 101 101 101 000 000 000 000 000 000 010 000 000

Ein Computer schreibt natürlich keine Zwischenräume und macht auch keine Zeilenumbrüche; die habe ich nur hinzugefügt, damit du die Darstellung leichter kontrollieren kannst! Die Breite und die Höhe des Bildes sowie die Farbcodierung muss man auch immer mit dazu schreiben oder dem Computer auf irgend eine Weise zugänglich machen, wenn man das Bild aus den vielen Nullen und Einsen richtig wieder herstellen will. Wie man dem Computer eine Farbe mitteilt, steht in Kapitel 5.3, in dem es um den Monitor geht.

Wir haben also jetzt eine Möglichkeit gefunden, auch Bilder nur mit Hilfe von Nullen und Einsen darzustellen.

Die Darstellung eines Bildes auf die oben beschriebene Weise nennt man eine Bitmap. Das ist Englisch und bedeutet so viel wie eine Landkarte von Bits.

Dir ist sicherlich aufgefallen, dass wir selbst für ein ganz einfaches Bild ziemlich viele Nullen und Einsen gebraucht haben!
Das Bild aus Abbildung 12 ist mit richtigen Pixeln gezeichnet so klein: 
Daran erkennst du wie viele Bytes man für ein größeres Bild braucht! Das ist ein grundsätzliches Problem bei Bildern, dass sie viel Platz für ihre Darstellung brauchen. Noch schlimmer ist es bei Filmen, bei denen man ca. 25 Bilder für eine Sekunde Film braucht, wenn er flüssig dargestellt werden soll! Man hat deshalb andere Verfahren entwickelt, wie man die Bilder (und im Übrigen auch alle anderen binären Daten, also alles was mit Nullen und Einsen dargestellt werden kann) Platz sparender darstellen kann - aber natürlich immer noch ausschließlich durch Nullen und Einsen!

Um dir zu zeigen, dass auch unser van-Gogh-Bild am Bildschirm aus Punkten zusammengesetzt wird, habe ich Vincents rechtes Auge einmal stark vergrößert. Abbildung 13 zeigt links das Bild, das du schon kennst, mit der Markierung der Stelle, die rechts vergrößert dargestellt wird.

Man kann gut erkennen, dass die Bildpunkte noch viel kleiner sind als die Farbkleckse, die van Gogh selbst verwendet hat. Die Größe eines einzelnen Pixels ist in der Vergrößerung rot markiert.

Abbildung 13: van Gogh stark vergrößert zur Verdeutlichung der Bildpunkte

Denken wir einmal darüber nach, was die Darstellung eines Bildes mit Hilfe so vieler kleiner Punkte und der den Farben zugeordneten Nullen und Einsen bedeutet:

Es ist doch zum Beispiel super einfach geworden, ein Bild verkleinert darzustellen! Wenn man zum Beispiel jeden zweiten Bildpunkt, bzw. jede zweite Spalte und jede zweite Zeile einfach nicht darstellt, ist das Bild nur noch ein Viertel so groß.
Zum Vergrößern des Bildes braucht man nur Zeilen und Spalten von Bildpunkten einzufügen, und die neuen Pixel in einer Farbe darzustellen, die so ähnlich ist wie die benachbarten Original-Pixel.
Wenn ich das Bild spiegeln will, brauche ich die Bildpunkte nur zeilenweise von rechts nach links zu lesen statt von links nach rechts, und wenn ich es auf den Kopf stellen will, brauche ich beim Lesen nur mit der letzten statt mit der ersten Zeile anfangen.

Besonders einfach ist das Ändern der Farben eines Bildes: Dafür muss man nicht einmal das Bild anfassen, sondern nur die Zuordnungstabelle, die festlegt, welches Bitmuster welcher Farbe entspricht (im Beispiel Tabelle 7).

Andererseits hat die Methode mit den Pixeln auch Nachteile: Wenn man ein Bild stark vergrößert, werden die Pixel sichtbar (wie in Abbildung 13) und das will man meistens nicht. Außerdem sind gerade Linien, die nicht genau senkrecht oder waagerecht durch das Bild laufen, keine Linien sondern Treppen, und das sieht man auch schon bei kleinen Vergrößerungen. Diese Linie ist ein Beispiel:

Ein weiterer Nachteil ist, dass man sehr schlecht bestimmte Bildinhalte gezielt verändern kann. Nehmen wir an, wir wollten Vincents Ohr größer machen! Wir können die Begrenzungslinie des Ohrs nicht als Ganzes ansprechen (also zum Beispiel darauf klicken und die ganze Linie ist markiert), sondern müssen alle Pixel, die dazu gehören, selbst auswählen.

Wegen dieser Nachteile hat man noch ein anderes Verfahren gefunden, um Bilder mit Nullen und Einsen zu beschreiben, die so genannte Vektorgrafik. Vektor kommt aus dem Lateinischen und bedeutet zu deutsch "Zeiger".

Natürlich braucht man wie immer eine Zuordnungstabelle, in der die Bedeutung der Nullen und Einsen festgelegt wird. Nur werden jetzt nicht Farben zu Bildpunkten zugeordnet sondern die Nullen und Einsen stehen für bestimmte Formen: Die Bildbeschreibung ist so aufgebaut, dass Figuren beschrieben werden. Das könnte in unserer Sprache zum Beispiel so aussehen:

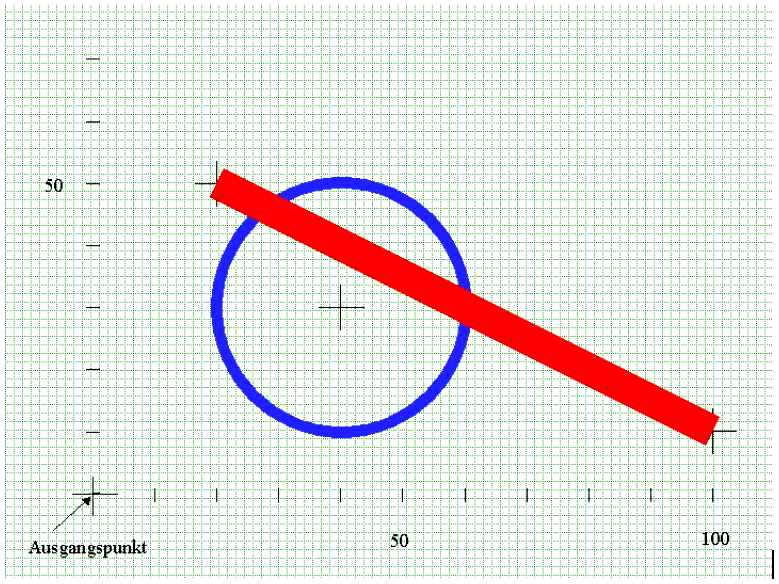
Kreis, Mittelpunkt 40 Bildpunkte nach rechts, 30 nach oben, Radius 20 Bildpunkte, Liniendicke 2 Bildpunkte, Linienfarbe 0011, nicht ausgefüllt.
Gerade Linie, Beginn 20 Bildpunkte nach rechts, 50 Bildpunkte nach oben, Ende 100 Bildpunkte nach rechts, 10 Bildpunkte nach oben, Liniendicke 5 Bildpunkte, Linienfarbe 0101

usw.

Das oben beschriebene Bild würde dann so aussehen:

Abbildung 14: Beispiel für eine Vektorgrafik

Dabei sind das grüne Raster im Hintergrund, die dünnen schwarzen Striche und die Zahlen nur eine Hilfe für dich, damit du die Bildpunkte leichter zählen kannst, um die Beschreibung nachvollziehen zu können! (Ein Kästchen entspricht einem Bildpunkt.) Die Linienfarbe 0011 entspricht in diesem Beispiel blau, 0101 entspricht rot.

So etwas lässt sich dann wieder mit Hilfe von Zuordnungstabellen in Nullen und Einsen übersetzen: Für "Kreis", "Gerade" und alle anderen Formen, die man zeichnen können soll, gibt es ein Bitmuster. Das Programm, das die Bildbeschreibung später liest, muss wissen, wie viele Eigenschaften einer Figur jeweils genannt werden und wie sie dargestellt werden. Solche Festlegungen nennt man auch ein Format. Eine Eigenschaft der Figuren ist natürlich auch die Farbe, die wieder in einer eigenen Tabelle festgelegt und durchnummeriert werden.

Eine Vektorgrafik hat den Vorteil, dass man sie beliebig vergrößern kann, ohne dass die Bildpunkte größer werden. Man rechnet beim Vergrößern einfach alle Bildpunktangaben für die größere Darstellung aus. Der Kreis im obigen Beispiel hätte bei einer vierfachen Vergrößerung (Verdopplung von Länge und Breite des Bildes) seinen Mittelpunkt bei 140 Bildpunkten nach rechts und 100 Bildpunkten nach oben und einen Radius von 80 Bildpunkten. Erst wenn diese Werte ausgerechnet sind, zeichnet das Programm den Kreis. - Der wird dann natürlich trotzdem wieder mit den Bildpunkten des Bildschirms dargestellt.

Man kann bei einer solchen Darstellung natürlich sehr leicht die Eigenschaften des Kreises ändern und ihm z.B. eine andere Farbe geben, weil man sich nicht alle Pixel zusammensuchen muss, die dazu gehören, sondern einfach nur die Farbangabe ändern muss.

Die Darstellung eines Bildes auf dem Bildschirm oder dem Drucker passiert aber immer mit Hilfe von Bildpunkten. Und weil du so tapfer bis hier hin die graue Theorie gelesen hast, machen wir dazu wieder ein kleines Experiment mit deinem PC:

Experiment 2:
Bildpunkte und Farben auf dem Monitor

Wenn die folgenden Erklärungen bei deinem Rechner überhaupt nicht stimmen sollten, frage bitte einen Erwachsenen, ob er dir die Bildschirmeinstellungen zeigen kann. Kleinere Abweichungen in der Darstellung sind aber möglich und kein Grund zur Panik! Störe dich nicht an unbekannten Begriffen in der Beschreibung; du wirst sie später noch lernen!

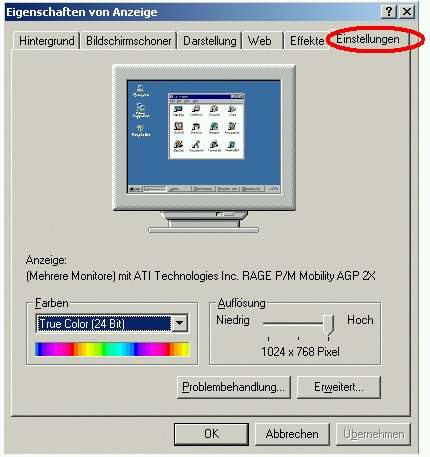
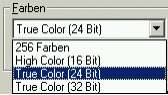Hier findest du genau das, worüber wir die ganze Zeit geredet haben: Unter "Farben" ist ein Auswahlfeld, das sich öffnet, wenn du auf den kleinen Pfeil klickst. (Man nennt das ein Drop-Down-Feld, weil es beim Öffnen quasi nach unten fällt.)
In diesem Feld kannst du auswählen, wie viele verschiedene Farben dein Bildschirm darstellen können soll. Bei der Einstellung "256 Farben" wird genau wie oben beschrieben für jeden Bildpunkt ein Byte benutzt, um die Farbe des Pixels festzulegen. Bei den anderen Einstellungen steht es schon dahinter: 16 Bit, also zwei Byte pro Bildpunkt, ermöglichen die Darstellung von 65536 verschiedenen Farben, bei 24 Bit, also drei Byte sind es schon 16.777.216 verschiedene Farben und bei 32 Bit oder vier Byte 4.294.967.296, also über vier Milliarden verschiedene Farben! Bestimmt mehr als das menschliche Auge überhaupt unterscheiden kann!
Warum kann man das überhaupt einstellen, wie viele Byte man pro Bildpunkt nehmen möchte, um die Farbe zu beschreiben? Warum nimmt man nicht einfach die beste Darstellung, also die mit 32 Bit? Nun, das ist ganz einfach: Die Farbe, die jeder einzelne Bildpunkt haben soll, muss ja auch irgendwo ausgerechnet werden, und das ist umso schwieriger und dauert um so länger, je mehr Farben es gibt, und je mehr Bildpunkte man hat.
Mehr Bildpunkte? Wo stellt man das denn ein? Unter dem Wort "Auflösung"! Wie fein ein Bild für seine Darstellung durch Bildpunkte unterteilt wird, bezeichnet man als Auflösung. Je mehr Bildpunkte, desto besser die Auflösung.

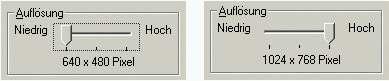
Auf meinem Computer kann man Einstellungen zwischen 640x480 und 1024x768 Bildpunkten vornehmen. In der guten Auflösung sind das also 786.432 Pixel. Wenn ich für jedes Pixel vier Bytes für die Farbfestlegung benutze, sind das immerhin 3.145.728 Bytes, oder 25.165.824, also über 25 Millionen Bits (und jedes Bit ist in unserem Computermodell ein Schalter!), die ich nur dafür brauche, den Bildschirm darzustellen.

Nun hast du Gelegenheit gehabt, nachzusehen, dass die Geschichte mit dem Darstellen der Bilder im Computer wirklich so einfach funktioniert, wie wir das in den Beispielen zuvor schon gesehen haben.

Du solltest das unter Punkt 4 des Experiments gezeigte Fenster mit "Abbrechen" schließen. Dann bleiben die Einstellungen deines Computers unverändert.