 |
3. Nullen und Einsen |
In der Einführung stand so eine komische Andeutung, dass all die tollen Sachen, die du vielleicht schon mit deinem Computer gemacht hast, wie Bilder malen, Texte schreiben, usw. für den Computer auch nichts anderes ist als rechnen mit Nullen und Einsen.
In den vorangegangenen Kapiteln haben wir ja schon gesehen, wie der Computer Zahlen mit Nullen und Einsen darstellt (vgl. Tabelle 2 bis Tabelle 5). Einer bestimmten Bitfolge wird eine bestimmte Zahl zugeordnet - sinnvoller Weise natürlich so, dass es auch mathematisch sinnvoll ist, nämlich auf die selbe Weise, wie wir auch im Dezimalsystem zählen.
Es hindert uns doch niemand daran, einer Bitfolge statt einer Zahl einen Buchstaben zuzuordnen, oder? Warum soll 01000001 nicht "A" bedeuten statt "65"?
Betrachten wir noch einmal die Addition (das Plus-Rechnen), die unser Super-Einfach-Computer im Abschnitt 3.1 durchgeführt hat: Das Ergebnis, also welche Lampe wann geleuchtet hat, hing doch nur davon ab, wie die Schalter gestellt waren, also welche Eingabe wir gemacht haben, und davon, wie unser Computer verdrahtet - man könnte auch sagen programmiert - war. Für die Schaltung war es völlig egal, welche Bedeutung wir den Schalterstellungen oder dem Leuchten der Lampe(n) zugeordnet haben; sie hat den Strom so geführt, wie eben die Verdrahtung war. Nur wir waren es, die die Verdrahtung genau so gemacht haben, dass die Bedeutung unseres Ergebnisses zur Bedeutung unserer Eingabe gepasst hat! Das hört sich jetzt an wie geschummelt, ist es aber nicht! Genau so arbeitet auch ein echter Computer!
Wir können uns doch jetzt eine einfache Aufgabe für die Bearbeitung von Texten einfallen lassen, zum Beispiel könnten wir aus einem großen Buchstaben einen kleinen Buchstaben machen wollen und umgekehrt. Damit unser Computer das kann, müssen wir nur festlegen, welches Bitmuster welchem Buchstaben entspricht, und müssen uns danach eine Verdrahtung überlegen, die bei jedem Großbuchstaben-Bitmuster an der Eingabeseite (Schalter) das zugehörige Bitmuster des Kleinbuchstabens an der Ausgabeseite (Lampen) erzeugt, bzw. umgekehrt.
Das ist einfacher als es sich anhört!
Fangen wir mit der Festlegung der Buchstaben an: Wenn wir bei den acht Bit bleiben, auf die sich die Erfinder des Computers irgendwann geeinigt haben, dann können wir 256 verschiedene Zeichen darstellen. Das Alphabet hat 26 Buchstaben; die gibt es als große und kleine Buchstaben, das macht zusammen schon mal 52 Stück. Dann kommen noch die Umlaute ä, ö und ü in groß und klein sowie das "ß" hinzu. Vermutlich werden wir auch mal ganze Sätze mit unserem Computer schreiben wollen; dafür brauchen wir dann auch noch Satzzeichen wie Punkt, Komma, Ausrufungszeichen, usw. und bestimmt finden wir es irgendwann toll, auch so komische Zeichen wie %, §, $, & benutzen zu können. Außerdem gibt es mit Sicherheit auch noch Computerfreunde in anderen Ländern, die noch weitere besondere Zeichen brauchen. Aber für den Anfang werden uns 256 Zeichen erst mal genügen!
Es ist sinnvoll, dass alle Computer die selbe Zuordnung von Buchstaben zu Bitfolgen verwenden, denn sonst hätte ein Text, den man auf dem einen Computer geschrieben hat, auf einem anderen Computer eine ganz andere Bedeutung und dieser Satz sähe vielleicht so aus:
Kl43jsdc l rlk 2ehr Es'fhg e4$" öoijh rfghElSöfdh verjhgo i reobjGRnSh oer ergPner oer rönkFGbjs.renor ihg9h 25QQnön548p 5gi uARsfd
Damit das nicht passiert, hat man sich auf die gemeinsame Festlegung in Tabelle 6 geeinigt, die man ASCII genannt hat.
ASCII ist dabei eine Abkürzung und bedeutet "American Standard Code for Information Interchange". Das ist Englisch und bedeutet auf Deutsch: Amerikanischer Standard Code für den Informationsaustausch. Obwohl in dem Namen "Amerikanisch" steht, benutzt man das auf der ganzen Welt.
Ein Code ist eine Zuordnung von Zeichen zu anderen Zeichen oder zu einer bestimmten Bedeutung.
| 0 | 0000 | 32 | 100000 | 33 | 100001 | ! | ||||
| 34 | 100010 | " | 35 | 100011 | # | 36 | 100100 | $ | ||
| 37 | 100101 | % | 38 | 100110 | & | 39 | 100111 | ' | ||
| 40 | 101000 | ( | 41 | 101001 | ) | 42 | 101010 | * | ||
| 43 | 101011 | + | 44 | 101100 | , | 45 | 101101 | - | ||
| 46 | 101110 | . | 47 | 101111 | / | 48 | 110000 | 0 | ||
| 49 | 110001 | 1 | 50 | 110010 | 2 | 51 | 110011 | 3 | ||
| 52 | 110100 | 4 | 53 | 110101 | 5 | 54 | 110110 | 6 | ||
| 55 | 110111 | 7 | 56 | 111000 | 8 | 57 | 111001 | 9 | ||
| 58 | 111010 | : | 59 | 111011 | ; | 60 | 111100 | < | ||
| 61 | 111101 | = | 62 | 111110 | > | 63 | 111111 | ? | ||
| 64 | 1000000 | @ | 65 | 1000001 | A | 66 | 1000010 | B | ||
| 67 | 1000011 | C | 68 | 1000100 | D | 69 | 1000101 | E | ||
| 70 | 1000110 | F | 71 | 1000111 | G | 72 | 1001000 | H | ||
| 73 | 1001001 | I | 74 | 1001010 | J | 75 | 1001011 | K | ||
| 76 | 1001100 | L | 77 | 1001101 | M | 78 | 1001110 | N | ||
| 79 | 1001111 | O | 80 | 1010000 | P | 81 | 1010001 | Q | ||
| 82 | 1010010 | R | 83 | 1010011 | S | 84 | 1010100 | T | ||
| 85 | 1010101 | U | 86 | 1010110 | V | 87 | 1010111 | W | ||
| 88 | 1011000 | X | 89 | 1011001 | Y | 90 | 1011010 | Z | ||
| 91 | 1011011 | [ | 92 | 1011100 | \ | 93 | 1011101 | ] | ||
| 94 | 1011110 | ^ | 95 | 1011111 | _ | 96 | 1100000 | ` | ||
| 97 | 1100001 | a | 98 | 1100010 | b | 99 | 1100011 | c | ||
| 100 | 1100100 | d | 101 | 1100101 | e | 102 | 1100110 | f | ||
| 103 | 1100111 | g | 104 | 1101000 | h | 105 | 1101001 | i | ||
| 106 | 1101010 | j | 107 | 1101011 | k | 108 | 1101100 | l | ||
| 109 | 1101101 | m | 110 | 1101110 | n | 111 | 1101111 | o | ||
| 112 | 1110000 | p | 113 | 1110001 | q | 114 | 1110010 | r | ||
| 115 | 1110011 | s | 116 | 1110100 | t | 117 | 1110101 | u | ||
| 118 | 1110110 | v | 119 | 1110111 | w | 120 | 1111000 | x | ||
| 121 | 1111001 | y | 122 | 1111010 | z | 123 | 1111011 | { | ||
| 124 | 1111100 | | | 125 | 1111101 | } | 126 | 1111110 | ~ | ||
| 161 | 10100001 | ¡ | 162 | 10100010 | ¢ | 163 | 10100011 | £ | ||
| 164 | 10100100 | ¤ | 165 | 10100101 | ¥ | 166 | 10100110 | ¦ | ||
| 167 | 10100111 | § | 168 | 10101000 | ¨ | 169 | 10101001 | © | ||
| 170 | 10101010 | ª | 171 | 10101011 | « | 172 | 10101100 | ¬ | ||
| 173 | 10101101 | | 174 | 10101110 | ® | 175 | 10101111 | ¯ | ||
| 176 | 10110000 | ° | 177 | 10110001 | ± | 178 | 10110010 | ² | ||
| 179 | 10110011 | ³ | 180 | 10110100 | ´ | 181 | 10110101 | µ | ||
| 182 | 10110110 | ¶ | 183 | 10110111 | · | 184 | 10111000 | ¸ | ||
| 185 | 10111001 | ¹ | 186 | 10111010 | º | 187 | 10111011 | » | ||
| 188 | 10111100 | ¼ | 189 | 10111101 | ½ | 190 | 10111110 | ¾ | ||
| 191 | 10111111 | ¿ | 192 | 11000000 | À | 193 | 11000001 | Á | ||
| 194 | 11000010 | Â | 195 | 11000011 | Ã | 196 | 11000100 | Ä | ||
| 197 | 11000101 | Å | 198 | 11000110 | Æ | 199 | 11000111 | Ç | ||
| 200 | 11001000 | È | 201 | 11001001 | É | 202 | 11001010 | Ê | ||
| 203 | 11001011 | Ë | 204 | 11001100 | Ì | 205 | 11001101 | Í | ||
| 206 | 11001110 | Î | 207 | 11001111 | Ï | 208 | 11010000 | Ð | ||
| 209 | 11010001 | Ñ | 210 | 11010010 | Ò | 211 | 11010011 | Ó | ||
| 212 | 11010100 | Ô | 213 | 11010101 | Õ | 214 | 11010110 | Ö | ||
| 215 | 11010111 | × | 216 | 11011000 | Ø | 217 | 11011001 | Ù | ||
| 218 | 11011010 | Ú | 219 | 11011011 | Û | 220 | 11011100 | Ü | ||
| 221 | 11011101 | Ý | 222 | 11011110 | Þ | 223 | 11011111 | ß | ||
| 224 | 11100000 | à | 225 | 11100001 | á | 226 | 11100010 | â | ||
| 227 | 11100011 | ã | 228 | 11100100 | ä | 229 | 11100101 | å | ||
| 230 | 11100110 | æ | 231 | 11100111 | ç | 232 | 11101000 | è | ||
| 233 | 11101001 | é | 234 | 11101010 | ê | 235 | 11101011 | ë | ||
| 236 | 11101100 | ì | 237 | 11101101 | í | 238 | 11101110 | î | ||
| 239 | 11101111 | ï | 240 | 11110000 | ð | 241 | 11110001 | ñ | ||
| 242 | 11110010 | ò | 243 | 11110011 | ó | 244 | 11110100 | ô | ||
| 245 | 11110101 | õ | 246 | 11110110 | ö | 247 | 11110111 | ÷ | ||
| 248 | 11111000 | ø | 249 | 11111001 | ù | 250 | 11111010 | ú | ||
| 251 | 11111011 | û | 252 | 11111100 | ü | 253 | 11111101 | ý | ||
| 254 | 11111110 | þ | 255 | 11111111 | ÿ |
Tabelle 6: Der ASCII-Code
Lass dich von der Tabelle nicht verwirren! Jeweils drei Spalten, die durch einen Abstand getrennt sind, gehören zusammen: Links steht die Dezimalzahl, dann kommt das Bitmuster aus acht Bit, das dieser Zahl entspricht, und in der dritten Spalte steht der Buchstabe oder das Zeichen, das man dem Bitmuster zugeordnet hat.
Unsere Buchstaben A bis Z bzw. a bis z findest du in dem blau hinterlegten Bereich.
Wenn du aufmerksam hinsiehst, wirst du merken, dass gar nicht alle 256 möglichen Bitmuster in der Tabelle gezeigt sind (z.B. 1 bis 31 nicht). Das liegt daran, dass diese mit etwas belegt sind, das man gar nicht drucken kann, zum Beispiel Zeichen, die einem Drucker sagen, dass er ein neues Blatt nehmen oder eine neue Zeile beginnen soll. So etwas nennt man Steuerzeichen.
Das Zeichen, das der Null zugeordnet ist und das Zeichen für 32 sehen in der Tabelle zwar gleich aus, sind sie aber nicht: Die Null bedeutet wirklich Nichts, und 32 ist der Code für ein Leerzeichen.
Noch etwas komisches fällt dir vielleicht an der Tabelle auf: Sie enthält auch Bitfolgen, denen die Ziffern 0 bis 9 zugeordnet sind. Sie stehen in dem mit gelb hinterlegten Bereich.
Wofür brauchen wir das denn? Wir haben doch im Kapitel 3.2 schon Zahlen durch Nullen und Einsen dargestellt! Warum machen wir das hier noch einmal, und noch dazu mit einer anderen Zuordnung als wir sie vorher hatten? Die "9" ist in der ASCII-Tabelle "00111001" und nicht "00001001", wie wir sie beim Rechnen geschrieben hätten! Nun die Antwort ist die: Auch beim Schreiben eines Textes wollen wir ja unsere Ziffern schreiben können; allein in diesem Absatz, den du gerade gelesen hast, kommen die Ziffern 0, 1, 2, 3 und 9 vor, aber rechnen im eigentlichen Sinne wollen wir damit ja gar nicht. Immerhin waren die Leute, die sich die ASCII-Tabelle ausgedacht haben, so schlau, dass die rechte Hälfte (das rechte Nibble) der Bytes, mit denen Ziffern dargestellt werden, identisch ist mit der mathematischen Codierung der Zahlen: Die rechten vier Bits des ASCII-Codes für die 9 heißen 1001 und das entspricht genau dem Muster, das entsteht, wenn wir mit Nullen und Einsen bis Neun zählen. Hexadezimal geschrieben (vgl. Kapitel 3.3!) ist der ASCII-Code für die Ziffern 0 bis 9: 0x30, 0x31, 0x32, ..., 0x39; die rechte Stelle der Hexadezimalzahl entspricht also immer der dargestellten Ziffer.
Zurück zu unserer Aufgabe: Unser Computer soll das Bitmuster eines Großbuchstabens in das Bitmuster eines Kleinbuchstabens umrechnen. Auch hier lohnt es sich genauer hinzusehen: Groß- und Kleinbuchstaben sind in ihrem Bitmuster identisch, außer an der sechsten Stelle von rechts! Großbuchstaben haben dort eine Null, Kleinbuchstaben eine Eins stehen.
Der Computer, der unsere Aufgabe bewältigen kann, muss also nur das Bitmuster von unseren acht Eingabeschaltern auf die Ausgabelampen übertragen. Lampe Nummer Sechs muss dabei leuchten, wenn auf der Eingabeseite eine 0 steht und ausgeschaltet sein, wenn dort eine 1 steht.
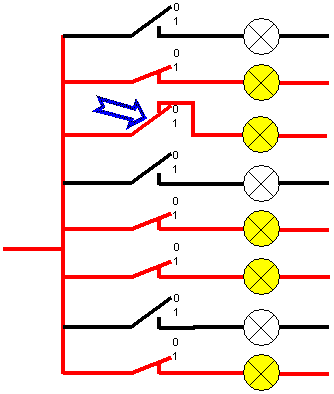
Abbildung 9 zeigt einen Computer der das kann. Dargestellt ist die Umrechnung von "M" in "m". (Suche das Bitmuster für m und für M in Tabelle 6!)
|
|
Abbildung 9: Computer, der von Groß- auf Kleinbuchstaben umrechnet und umgekehrt |
Beachte:
Der Schalter für Bit Nr. 6 (Pfeil) steht in Stellung "Null" also oben. Trotzdem leitet er den Strom. Würden wir von "m" in "M" umrechnen, müssten wir diesen Schalter nach unten in Stellung "Eins" drücken; in dieser Stellung wäre das Kabel dann unterbrochen, so dass auf der Ausgabeseite eine Null erscheint. Man sagt das Bit wird invertiert, also umgedreht: Am Ausgang (Lampe) steht immer das Gegenteil vom Eingang (Schalter).
Eine zweite Besonderheit: Eigentlich bräuchte unser Computer für diese Aufgabe nur sechs Schalter und sechs Lampen, weil die Bits Nummer 7 und Nummer 8 sowohl bei Groß-, als auch bei Kleinbuchstaben immer auf Null bzw. Eins stehen (vgl. Tabelle 6). Wenn du unseren Computer wirklich benutzen und mit den Schaltern Buchstabencodes eingeben würdest, könntest du feststellen, dass du diese beiden Schalter nie verstellen müsstest.
Und in der Tat: Alte Fernschreiber, das sind Geräte mit denen man früher Texte über eine Telefonleitung übertragen hat, haben nur mit fünf Bit gearbeitet: Sie haben nicht zwischen Groß- und Kleinschreibung unterschieden und konnten mit fünf Bit 32 verschiedene Zeichen darstellen. Heute braucht man diese Geräte nicht mehr; das Telefax hat sie völlig verdrängt!
Unser Computer zur Umrechnung von Groß- auf Kleinschreibung und umgekehrt funktioniert jedenfalls!
Das war jetzt ziemlich viel Theorie und wahrscheinlich glaubst du noch gar nicht, dass so etwas in einem echten Computer auch so geht. Wenn du einen PC hast, kannst du es gleich ausprobieren! Lass dir von jemandem helfen, wenn dir die Anleitung nicht klar ist, oder lies erst weiter; alles was dir fremd vorkommt und du nicht verstehst, wird später noch erklärt!
Experiment 1:
ASCII-Codes sind im PC versteckt!
Wo welche Taste sitzt, wird in Abbildung 10 gezeigt!
|

|
| Abbildung 10: PC-Tastatur |
Wenn du bei diesem Versuch ASCII-Codes verwendest, die größer sind als 127, kann es vorkommen, dass du andere Zeichen angezeigt bekommst als in Tabelle 6 gezeigt sind. Das liegt daran, dass es von dieser oberen Hälfte der Tabelle (Code Nummer 128 bis 255) verschiedene Versionen gibt, weil man mit den 255 möglichen Zeichen doch nicht ausgekommen ist, und man diesen Teil der Zuordnungen wechseln kann.
Was zeigt uns dieser Versuch? Nun: Der Computer interpretiert deine Zahleneingabe entsprechend der in Tabelle 6 gezeigten Zuordnung. Man hat sie ihm also einprogrammiert. Früher hat man dieses Verfahren mit der Alt-Taste gebraucht, um dem Computer Zeichen einzugeben, die nicht auf der Tastatur stehen. Heute bietet fast jedes Programm eine bequemere Möglichkeit, solche Sonderzeichen einzugeben.
Aber immerhin bist du jetzt sicher, dass dein Computer unsere Zuordnung der Buchstaben und Zeichen zu den Nullen und Einsen richtig versteht!
Noch ein kleiner Hinweis: Obwohl du mit dem Ziffernblock die selben Zahlen eingibst wie mit den anderen Zifferntasten unterscheidet dein Computer diese Tasten! Das kannst du daran erkennen, dass das Experiment mit den anderen Zifferntasten nicht funktioniert!
| 3.3 Bits und Bytes für Menschen - Das 16er-System | Inhaltsverzeichnis Index |
3.5 Bilder mit Nullen und Einsen |